Table of Contents
Discover the truth about Is Linear Algebra Hard. Explore key factors that make linear algebra challenging and find tips to conquer this fundamental mathematical subject.
Linear algebra is considered one of the most challenging undergraduate math courses by many students. The high level of abstraction, theoretical concepts, and new computational skills required can make linear algebra seem impenetrable at first. However, with the right strategies and perspective, it is possible to master this essential subject. In this article, we’ll dive into the key reasons why Linear Algebra Hard poses such a stiff challenge for beginners and provide tips to help you succeed in grasping this fascinating branch of mathematics.
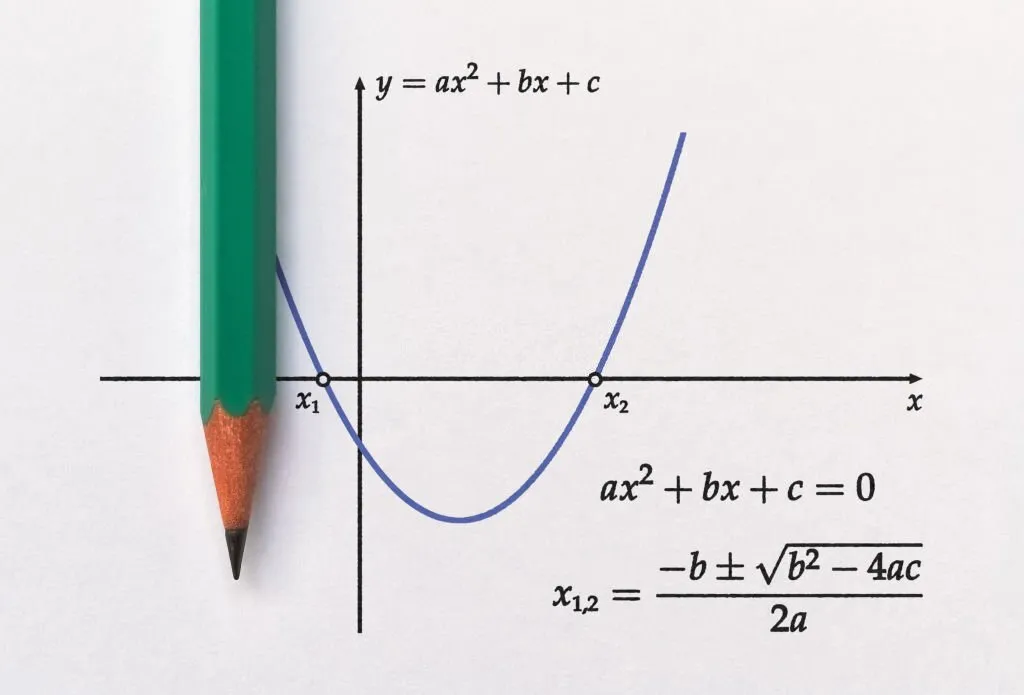
Why Is Linear Algebra Hard?
There are several core reasons why Is Linear Algebra Hard presents a unique challenge compared to other math subjects:
1. Highly Abstract Concepts
Linear algebra deals with vectors, vector spaces, linear transformations, and other abstract mathematical constructs. Unlike calculus and statistics, there are no graphs to draw or datasets to visualize. Linear algebra requires you to conceptualize theoretical vector spaces and perform manipulations in your mind without tangible coordinates.
Trying to understand concepts like spanning, linear independence, basis vectors, and dimensionality is extremely abstract. The ability to visualize these ideas geometrically can help provide intuition, but it requires practice in developing a whole new mathematical way of thinking.
2. New Kinds of Mathematical Skills
In addition to abstract concepts, Is Linear Algebra Hard requires you to learn new technical skills including:
- Matrix arithmetic operations like addition, multiplication, finding inverses and determinants
- Calculating eigenvalues and eigenvectors and diagonalization of matrices
- Understanding singular value decomposition and orthogonal projections
- Proving theorems about span, linear independence, and bases of vector spaces
- Translating word problems into linear systems and leveraging Gaussian elimination
Mastering these unique procedures and computational techniques takes time and practice. Having to simultaneously learn new skills and theory amplifies the challenge.
3. Applications May Seem Abstract Initially
While Is Linear Algebra Hard enables many useful applications, these connections to the real world aren’t necessarily obvious when you first learn the concepts. Applications such as Is Linear Algebra Hard:
- Data analysis techniques in machine learning and statistics
- Computer graphics transformations and projections
- Optimization problems in fields like engineering and economics
- Quantum mechanics principles and methods
Seem just as abstract as the mathematical concepts at first. It takes time to fully appreciate how vectors, matrices, and linear transformations form the foundation for these applications.
4. Very Different From Previous Math Experience
Most students first take calculus in high school, building on concepts learned in algebra and geometry. Linear algebra introduces a whole new way of thinking mathematically starting from scratch. The level of abstraction and lack of previous familiarity or intuition can be jarring. Having to rewire your brain to think about math from a blank slate requires time and discipline. Get more info about How hard is linear algebra compared to calculus.
Strategies for Mastering Linear Algebra
While Is Linear Algebra Hard poses many challenges, with the right outlook and techniques, it is very learnable. Here are study tips and strategies to help you master linear algebra:
1. Focus on Conceptual Understanding Before Computations
It’s easy to get overwhelmed trying to memorize formulas and mechanics of matrix operations before understanding what matrices represent. Prioritize grasping the higher-level concepts, purpose, and motivations first before diving into computations. Understand what vectors and matrices are and how they connect to real-world systems before working through dozens of practice problems.
2. Work Through Many Concrete Examples
Apply the abstract concepts and computations to tangible example problems to build intuition. For example, represent concepts like linear independence and spanning geometrically with visual depictions. Work through examples of transforming and analyzing images and data using matrix techniques. Leverage visuals and numerical problems to reinforce the theories.

3. Study Collaboratively: Is Linear Algebra Hard
Linear algebra is challenging and best learned collaboratively. Form study groups, compare notes with fellow students, and discuss concepts together. Explain tricky ideas to each other and work through practice problems as a team. You’ll gain new insights from peers that a lecturer or book can’t provide.
4. Ask Questions Frequently and Seek Help
Don’t bang your head trying to grasp fuzzy concepts alone! Ask questions in class, attend office hours and tutoring sessions, and get help early when ideas seem confusing. Finding other resources and explanations outside class is key. The faster you clarify shaky ground, the easier future concepts will be to absorb.
5. Be Patient and Persistent
Linear algebra won’t click after just a lecture or two. You have to be patient and stick with it! The payoff of finally grasping concepts after days or weeks of fuzzy confusion is so rewarding. Persist through the challenges and trust that your understanding will grow with time. Stay motivated knowing the payoff is immense.
The Reward Is Worth the Struggle
Learning linear algebra is a major milestone in your mathematical education. While requiring new ways of thinking, your mind expands with mathematical maturity once you master this subject. You gain access to the powerful toolkit enabling fields from machine learning to quantum physics. Appreciate linear algebra as a milestone marking your progression into advanced mathematics, computer science, and data science. With the right mindset and tenacity, you can develop insight into this empowering field!
How Hard Is Linear Algebra?
Linear algebra is a fundamental department of arithmetic that deals with vector spaces, linear equations, and the relationships among them. Many college students and rookies regularly marvel, “How difficult is linear algebra?” The trouble of linear algebra can vary from character to character, but numerous elements contribute to its perceived complexity.
1. Conceptual Depth: Linear algebra introduces summary concepts inclusive of vector spaces, matrices, determinants, and eigenvalues. Understanding those principles and their interrelationships can be hard for some people.
2. Abstract Thinking: Linear algebra calls for a degree of abstract wondering and mathematical reasoning that can be one-of-a-kind from different math courses. It involves manipulating symbols and equations to clear up troubles, which may be daunting for people who decide upon greater concrete arithmetic. Great Post read about autodidacts.
Why Is Linear Algebra So Hard?
Linear algebra is a fundamental branch of mathematics that deals with vector areas and linear equations. While it paperwork the premise for many scientific and engineering disciplines, it’s frequently taken into consideration as challenging for numerous reasons:
1. Abstract Concepts: Is Linear Algebra Hard introduces abstract concepts such as vector areas, subspaces, and linear variations. These thoughts can be hard to understand for people who are new to the difficulty.
2. Notable Abundance of Notation: Linear algebra employs numerous notations, along with matrices, vectors, and operations like matrix multiplication. Understanding and working with this notation can be overwhelming at the beginning.
3. Complex Operations: Solving systems of linear equations, locating eigenvalues and eigenvectors, and performing matrix operations can be elaborate and contain several steps.

FAQs
Q: What are some good strategies for visualizing abstract linear algebra concepts?
A: Leverage graphs, diagrams, animations, and 3D models to depict vectors, spanning, transformations, and other concepts. For example, show vectors as arrows and use different colors to distinguish linearly dependent vs. independent sets. Animations help visualize how matrices transform objects in space.
Q: Should I memorize formulas and mechanics or focus on high-level concepts first?
A: Prioritize grasping high-level concepts, purpose, and theory first before diving into computational details. Don’t get bogged down memorizing mechanics early on. Build conceptual grounding then reinforce with computations.
Q: Are there useful online resources for extra help learning Is Linear Algebra Hard?
A: Yes, sites like Khan Academy, Brilliant, and 3Blue1Brown have excellent linear algebra explainer videos and practice problems. Some even use interactive 3D visuals to depict concepts. Leverage these free resources to supplement your textbook and class.
Q: Is it manageable to take linear algebra and calculus concurrently?
A: It is doable for some but very challenging for most students. Covering two fundamentally different math topics simultaneously requires solid time management and mental bandwidth. Consider taking them in sequential semesters if possible.
Q: How does linear algebra connect to machine learning and data science applications?
A: Linear algebra provides foundational algorithms for machine learning like regression, dimensionality reduction, gradient descent, and neural networks. Matrix decompositions enable recommendation systems. Vector operations process data efficiently. Linear algebra is crucial for data science.

Liam Stephens is a dynamic and skilled blogger, recognized for his ability to identify trends and create compelling content. As the founder of Remi-Portrait.com, Liam has become a reliable source of information across various fields such as food, technology, health, travel, business, lifestyle, and current events. He specializes in delivering up-to-date technology news and insights, catering to the diverse community that surrounds Remi-Portrait.com. His proficiency and engaging writing style have earned him a dedicated audience, solidifying his reputation in the digital sphere.



